RC Phase-shift Oscillators

The basic RC phase shift oscillator comprises a single-stage amplifier whose output is fed back to its input through a feedback network. The amplifier portion is usually implemented by either a bipolar transistor-based common-emitter amplifier stage, FET-based common-source amplifier or an operational amplifier wired as an inverting amplifier. The feedback network comprises a cascade arrangement of three identical sections of either lag- or lead-type RC network.

Figure below shows the circuit schematic of an RC phase shift oscillator using a common-emitter amplifier stage and a lag-type RC feedback network.

RC phase shift oscillator using common-emitter amplifier and lag-type RC feedback network

Figure below shows another version of RC phase shift oscillator in which the amplifier portion is implemented using an inverting operational amplifier and a lag type RC feedback network.

RC phase shift oscillator using operational amplifier and lag type RC feedback network

In both cases, the amplifier provides a phase shift of 180^°at the frequency of operation. Therefore, which means that the feedback network must also provide an additional phase shift of 180^°at the operating frequency to satisfy the loop phase shift condition of the Barkhausen criterion. Also, the gain to be provided by the amplifier stage must at least equal the inverse of the attenuation factor of the feedback network.

In nutshell, in the phase shift oscillator, the amplifier gain is dictated by the feedback network attenuation factor and the phase shift provided by the amplifier stage decides the phase shift to be provided by the feedback network.

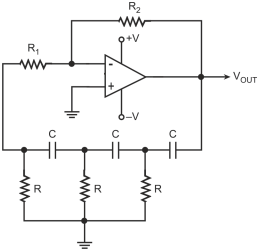
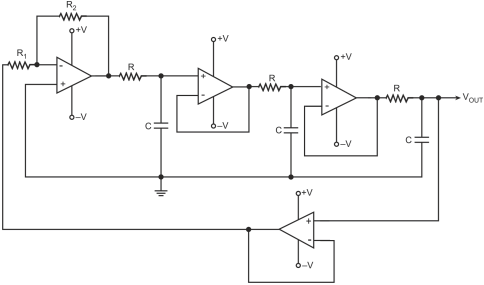
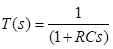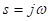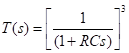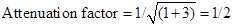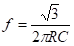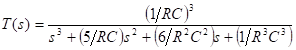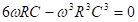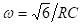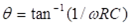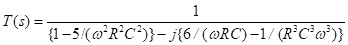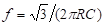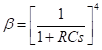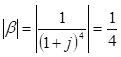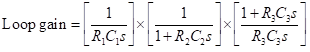The transfer function of a single-stage lag-type RC network is given by

Assuming that the RC sections in the cascade arrangement are independent of each other, that is, individual RC sections do not load each other, then the transfer function of the cascade arrangement of three sections is given by

Now, the single-section RC network provides a phase shift (Ø) given by

Therefore,

If this single RC section were to provide the desired phase shift of 60 ^° so as to produce a total phase shift of 180 ^°from the feedback network, then the operational frequency of the oscillator would be given by

Therefore,

Attenuation factor provided by single-section RC network at this frequency is given by

The overall attenuation factor (β) of the feedback network is then given by

β = (1/2)3 = 1/8

Therefore, the amplifier gain must at least be equal to 8.

In practice, the required gain is much higher than 8 and also that the oscillation frequency is also higher than

This is due to the loading effect of different RC sections, as explained below, when they are in cascade arrangement.

Considering the loading effect, the transfer function of the three-section RC network of the lag type is given by

Substituting

we get

Multiplying both numerator and denominator by R³C³, we get

If the feedback network were to provide an overall phase shift of 180 ^°, then the imaginary part should be equal to zero.

That is,

, which gives

Substituting this value of w, we get the expression for the feedback factor as

To summarize, in the case of a lag-type RC phase shift oscillator, the frequency of oscillation is given by f = [ √6/(2ΠRC)] and minimum amplifier gain is 29.

Figure below shows circuit schematic of RC phase shift oscillator using lead-type phase shift network.

Op-amp-based lead-type RC phase shift oscillator

Transfer function of single-section RC lead network is given by

Phase shift provided by single-section RC lead network is given by

Therefore,

Considering the loading effect, the transfer function for the cascade arrangement of three-section lead-type RC network is given by

If the feedback network were to provide an overall phase shift of 180 ^°, then the imaginary part should be equal to zero. That is,

Substituting the value of w, we get expression for the feedback factor:

To summarize, in the case of an lead-type RC phase shift oscillator, the frequency of oscillation is given by f = [1/(2Π √6RC)] and minimum amplifier gain is 29.

Three-section RC phase-shift oscillator have high d⊝/dw value resulting from steep phase versus frequency slope provided by the three-section RC network. This gives these oscillators reasonably high frequency stability.

RC phase shift oscillators are not used for constructing variable frequency oscillators as it is impractical to simultaneously vary three capacitance values equally. Also, adjustment of resistance values is not recommended because variation of resistance values will alter the loop gain of the oscillator circuit and there is likelihood of it not satisfying Barkhausen criterion for sustained oscillations.

The buffered RC phase shift oscillator overcomes the loading effect of different RC sections in the conventional phase shift oscillator. Figure below shows the circuit diagram of a lag-type buffered RC phase shift oscillator.

The oscillation frequency is given by

In the case of lead-type RC network, the oscillation frequency would be given by

The minimum value of the amplifier gain in both the lead-type and the lag-type configurations for sustained oscillations is 8.

Lag-type buffered RC phase shift oscillator

Bubba oscillator is a slight variation of the buffered RC phase shift oscillator as shown in figure below. The difference between the two is that the Bubba oscillator uses four RC sections in the feedback network with each RC section contributing a phase difference of 45. This offers the following two distinctive advantages. One, taking outputs from alternate sections yields low impedance quadrature outputs. Two, use of four RC sections provides higher d⊝/dw, which in turn leads to relatively higher frequency stability.

As we can see from the figure, different sections in the feedback network are buffered and therefore there is no loading effect Therefore, the expression for the transfer function of the feedback network is given by

Single-section RC section provides a phase shift of 45 ^° for  = 1/RC.

Substituting for w, we get

Therefore, the gain of the amplifier must at least be 4 for oscillations to occur.

Bubba oscillator

. Quadrature oscillator is a type of RC phase shift oscillator. Figure below shows the circuit schematic of the quadrature oscillator. As we can see from the figure, it employs three RC sections

We know that double integral of a sine wave is a negative sine wave of the same frequency and phase. This implies that the original waveform is 180 phase-shifted after double integration. The quadrature oscillator employs double integrator. The phase of the output from second integrator is then inverted to provide positive feedback to induce oscillations.

Quadrature oscillator

The transfer function of the feedback network is a cascade arrangement of three networks. The first one comprises R₁–C₁ configured around op-amp A₁. The second one comprises R₂–C₂ and the third one comprises R₃–C₃ configured around op-amp A₂. The expression for loop gain is given by

If R₁C₁ = R₂C₂ = R₃C₃ = RC and if we substitute w = 1/RC, the first network provides a phase shift of 90 °, the second and third networks provide phase shift of 45 ° so as to provide a total phase shift of 180 °. Op-amp A₁ too provides a phase shift of 180 °, which leads to loop phase shift of 0 °. Therefore, the loop gain is given by

Therefore, the oscillation frequency is

w = 1/RC

The circuit provides sine and cosine outputs (quadrature outputs) because of 90 ° phase difference between the two signals present at the outputs of the two op-amps.